社会网络分析及其可视化¶
社会网络分析¶
社会网络分析(Social Network Analysis, SNA)是一套用来研究“人与人、组织与组织之间关系结构”的方法。它重点不在个人本身,而在于关系:谁和谁联系、联系强弱如何、信息在关系网络中如何流动、哪些节点在网络中最重要等。
研究关系结构,而不是孤立的个体¶
社会网络分析把个体(人、组织、国家等)视为“节点”,把关系(合作、交流、交易、关注、信任等)视为“边”。
它主要回答的问题包括:
谁与谁联系得最紧密?
网络中有没有“核心人物”“关键组织”?
信息是怎样在网络中传播的?
哪些节点连接了原本不相连的群体?
衡量节点的重要性¶
SNA会计算一些指标来判断谁在网络中更关键,比如:
度中心性(Degree centrality):一个节点连接了多少人。
中介中心性(Betweenness):谁在网络中起“桥梁”作用。
接近中心性(Closeness):谁更容易接触到网络所有其他人。
特征向量中心性(Eigenvector):节点不仅自己重要,还连接重要的人。
这些指标可以用来识别“影响力者”“传播关键节点”等。
分析网络中的群体结构¶
SNA可以发现:
社会群体(比如朋友圈、合作圈)
组织内部的小群体或者部门壁垒
社群之间的联系强度
隐性关系或潜在合作路径
技术上通常用到聚类、社区发现等方法。
典型应用领域¶
社会网络分析非常广泛,常见于:
社交媒体分析(微博、推特上的关系、传播、意见领袖)
组织行为学(公司内部沟通分析、找出合作瓶颈)
公共卫生(疫情传播路径分析)
犯罪网络分析(揭示犯罪团伙的核心成员)
学术分析(合作网络、引用网络)
用户体验与语言服务领域(分析用户群体、知识传播结构)
案例背景¶
故事发生在 20 世纪 70 年代早期,地点是美国一所大学的校园空手道俱乐部。俱乐部成员之间除了训练,还经常一起参加聚会、外出和社交活动,因此形成了密集的社交网络。
研究者 Wayne W. Zachary 在 1970–1972 年间系统观察并记录了俱乐部内部:
谁与谁一起活动
成员之间的亲密程度
社交互动次数
他最终构建了一个 34 人的社交网络,每条边代表成员间的互动或友谊。
冲突的出现:俱乐部领导人与管理员意见不合¶
俱乐部有两个核心人物:
Instructor(教练)——网络数据中对应节点 0(不同论文编号略有差异)
Administrator(管理员)——对应 节点 33
他们在俱乐部的运营方式、课程费用和管理理念上产生了尖锐分歧。
随着时间推移,俱乐部成员开始在社交上“站队”:
喜欢教练的成员逐渐围绕教练形成一个社群
认同管理员的人围绕管理员形成另一群
这些倾向在网络结构中体现得非常明显,**两个社区在网络中自然形成,没有任何算法都能肉眼看出。**这就是它为什么成为 SNA 经久不衰的示范案例的原因。
最终结果:俱乐部分裂成两个组织¶
冲突升级后,俱乐部最终 正式分裂成两个独立的俱乐部。
成员分布如下:
一些成员选择跟随原教练,加入他新的俱乐部
另外一些成员留在原来的俱乐部,由管理员负责
真实世界的结果与 Zachary 收集的社交网络结构 高度吻合:
在网络里属于教练社区的人,大多数最终也选择了教练阵营
社区划分算法(例如 Girvan–Newman 或 Louvain)几乎可以 100% 准确预测成员最终选择
这使得该数据成为:
社会网络分析中“社区检测”的标杆教材
“社交结构如何预测行为”的最佳案例之一
网络分析过程¶
明确分析对象¶
Zachary 的研究对象:
节点:空手道俱乐部 34 名成员
边:成员之间在课外有交往(互动次数反映权重)
网络类型:无向、加权图
数据收集¶
Zachary 在 1970–1972 对俱乐部成员进行了 参与式观察:
记录成员之间的互动
记录共同出席活动
打分形成频率矩阵(interaction matrix)
最终得到 34×34 的邻接矩阵(或边列表)
指标分析¶
度中心性(Degree Centrality)¶
用于找“最受欢迎”或“最活跃”的成员。
在空手道俱乐部中:度中心性最高的人是 0 号(Mr. Hi)和 33 号(Club President John A)
这对应了:一个是教练,一个是管理员,两派领袖。
他们很重要,连边很多,是自然的中心人物。
介数中心性(Betweenness Centrality)¶
用于识别“桥梁人物”“分裂风险点”。
使用 Brandes 算法计算最短路径上的关键节点。
在空手道俱乐部中:
节点 2、1、3 等有高介数中心性
这些人并不是“最受欢迎”,但他们位于两派之间
他们的立场左右着俱乐部分裂的方向
社区检测(Community Detection)¶
算法:Girvan–Newman
步骤:
找介数最高的边
删除
再计算
不断迭代直到网络分裂成两块
在空手道数据上:
GN 算法自动把 34 个节点分成两群
结果与俱乐部实际后来的现实分裂高度吻合
可视化¶
用力导向算法(Fruchterman-Reingold 或 ForceAtlas2)绘图:
特点:
边多的节点会更靠近
关系密切的成员自然聚成团
两派显著分离
工具介绍¶
NetworkX (Python)¶
特点:最经典、最易用的社会网络分析库。
能做什么:中心性、路径、社区发现、图可视化等。
适合:教学、科研、小中规模网络(几十万节点以内)。
优势:简单易用,生态丰富,与 pandas/scikit-learn 深度融合。
功能¶
1. 创建并操作图结构 支持:
有向图
无向图
多重图(多条边)
自定义节点属性、边属性
import networkx as nx
G = nx.Graph()
G.add_node("A")
G.add_edge("A", "B")
2. 计算中心性指标(核心功能)
社会网络分析常用的所有指标都能算:
Degree centrality(度中心性)
Betweenness centrality(中介中心性)
Closeness centrality(接近中心性)
Eigenvector centrality(特征向量中心性)
PageRank(网页排名指标)
nx.betweenness_centrality(G)
3. 分析网络结构
最短路径
连通分量
聚类系数
图直径、平均距离
社区发现(基于 Girvan–Newman、Louvain 等)
4. 可视化
NetworkX 有基本可视化功能(但不如 Gephi 好看):
import matplotlib.pyplot as plt
nx.draw(G)
plt.show()
5. 与 Pandas、Numpy、Scikit-Learn 配合
可以从 CSV / DataFrame 直接构建图:
import pandas as pd
df = pd.read_csv("edges.csv")
G = nx.from_pandas_edgelist(df, source="source", target="target")
NLP / 文本处理背景的人,可以轻松用它分析:
词语共现网络
引文网络
学术合作网络
用户行为网络
技术写作系统中的术语传播网络
优缺点¶
优点:
入门简单,适合学习 SNA
Python 生态完善
小中规模图性能稳定(几十万节点以内)
文档齐全,科研论文中非常常见
缺点:
不适合处理特别大的图(上千万节点)
可视化能力不如 Gephi、Cytoscape
高性能需求时可换 igraph 或 Graph-tool
与Gephi的关系
工具 |
类型 |
用途 |
|---|---|---|
NetworkX |
Python 库 |
计算、建模、算法、数据处理 |
Gephi |
桌面可视化软件 |
绘图、美化、探索式分析 |
实际研究中常常这样组合使用:
用 NetworkX 读取与处理数据、计算指标
输出 GEXF 文件
用 Gephi 打开 GEXF 进行布局与可视化
nx.write_gexf(G, "network.gexf")
代码实现¶
0. 安装networkx¶
!pip install networkx
1. 加载空手道数据¶
import networkx as nx
G = nx.karate_club_graph()
print(G.number_of_nodes(), G.number_of_edges())
34 78
表示这个图中有 34 个节点(共 34 名成员参与了 Zachary 的研究),有 78 条边(总共有 78 对成员在研究期间被观察到有社交联系)
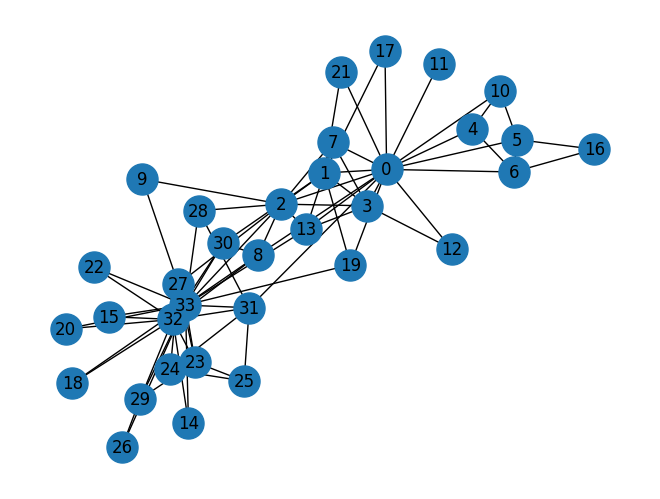
2. 可视化一个网络¶
import matplotlib.pyplot as plt
nx.draw(G, with_labels=True, node_size=500) #每个节点的面积大小为 500(像素的平方)左右
plt.show()
3. 计算度中心性(合作/连接最多的)¶
deg = nx.degree_centrality(G)
sorted(deg.items(), key=lambda x: -x[1])[:5]
nx.degree_centrality(G) 的输出是每个节点的 度中心性,公式为:
degree_centrality(node) = 该节点的度数 / (N - 1)
其中 N 是整个图的节点数量。
对于 Zachary 空手道俱乐部网络,N = 34,因此:
分母 (N−1) = 33。
[(33, 0.5151515151515151),
(0, 0.48484848484848486),
(32, 0.36363636363636365),
(2, 0.30303030303030304),
(1, 0.2727272727272727)]
节点 |
度中心性 |
解释 |
|---|---|---|
33 |
0.515 |
节点 33 与 17 个节点相连(17/33 ≈ 0.515)。它是全图最关键的“交往中心”,高度活跃,很可能是网络中的领导者或关键人物。 |
0 |
0.485 |
节点 0 与 16 个节点相连(16/33)。它也是非常核心的成员,是另一个主要中心节点。 |
32 |
0.364 |
与约 12 个节点相连(12/33)。属于比较重要但没有 33、0 那么关键的次级中心。 |
2 |
0.303 |
与约 10 个节点相连(10/33)。处于网络较显眼位置,但不是最中心的人。 |
1 |
0.273 |
与约 9 个节点相连(9/33)。属于较活跃的成员,但中心性进一步降低。 |
这和经典研究的结论一致:
节点 33 通常对应“Mr. Hi”阵营的核心
节点 0 对应“John A”阵营的核心
4. 介数中心性(“桥梁”角色)¶
bet = nx.betweenness_centrality(G)
sorted(bet.items(), key=lambda x: -x[1])[:5]
中介中心性(betweenness centrality) 衡量一个节点在网络中充当“桥梁”或“中间人”的程度。
公式的核心思想:
一个节点越多地位于其它节点之间的最短路径上,中介中心性越高。
因此:
高值 = 该节点对网络的连通、信息流动非常关键
移除高值节点通常会破坏网络结构、导致群体分裂
[(0, 0.43763528138528146),
(33, 0.30407497594997596),
(32, 0.145247113997114),
(2, 0.14365680615680618),
(31, 0.13827561327561325)]
节点 |
中介中心性 |
意义 |
|---|---|---|
0 |
0.438 |
处于最多最短路径上,是全图最关键的“桥梁节点”,在不同子群体之间起核心通道作用。 |
33 |
0.304 |
也是一个重要桥梁,但略弱于 0。仍是网络中核心领导者之一。 |
32 |
0.145 |
中等桥梁节点,连接了不同社区的重要路径。 |
2 |
0.144 |
和 32 类似,也是跨社区的次级桥梁。 |
31 |
0.138 |
在特定社群之间的最短路径上出现频繁,是隐含的中介角色。 |
5. PageRank(最被依赖/最“权威”的)¶
pr = nx.pagerank(G)
sorted(pr.items(), key=lambda x: -x[1])[:5]
PageRank 衡量的是:
一个节点的重要性取决于:
有多少节点指向它(连接数量)
指向它的节点本身是否重要(连接质量)
用一句话概括:
不仅要“朋友多”,还要“朋友的重要”。
因此,PageRank 代表的是一种“声望”或“影响力”指标。
[(33, 0.09698041880501741),
(0, 0.08850807396280014),
(32, 0.07592643687005646),
(2, 0.06276686454603017),
(1, 0.05741484049711006)]
节点 |
PageRank 值 |
含义 |
|---|---|---|
33 |
0.097 |
网络中声望最高的节点,具有最强的“影响力”。其他重要节点也倾向于连接它。 |
0 |
0.089 |
第二高影响力节点,位置重要性仅次于节点 33。 |
32 |
0.076 |
影响力稳固的中层核心节点。 |
2 |
0.063 |
连接数量与连接质量都不错,属于次中心。 |
1 |
0.057 |
虽然不如前几名核心,但仍属于重要成员。 |
度中心性前五是:
33, 0, 32, 2, 1
PageRank 前五也是:
33, 0, 32, 2, 1
这说明:
Karate Club 图的结构使得连接数量本身就能很好代表“重要性”
核心节点之间彼此互相连接,使 PageRank 权重也集中在它们身上
PageRank 是一种“加权的度中心性”,但这里网络本身具有明显核心结构,使得两者非常一致。
6.做简单社区划分¶
from networkx.algorithms.community import girvan_newman
communities = next(girvan_newman(G))
print([list(c) for c in communities])
这个算法通过 不断删除介数中心性最高的边,使网络自动分裂成多个社区。
高介数的边通常是“跨社区的桥梁边”。 当这些边被删掉后,网络会分成内部紧密、外部松散的两大块。
[[0, 1, 3, 4, 5, 6, 7, 10, 11, 12, 13, 16, 17, 19, 21], [2, 8, 9, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]]
社区 A(15 个节点)
[0, 1, 3, 4, 5, 6, 7, 10, 11, 12, 13, 16, 17, 19, 21]
中介中心性最高的是 node 0
他是俱乐部管理员,对多个子群体有连接
这个社区节点内部连接较密集,与社区 B 较少连接
社区 B(19 个节点)
[2, 8, 9, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]
节点 33 与大量节点直接相连,是训练师阵营的核心
他社区内部结构紧密,连接强度高
多个重要节点(32、31、2)支持这一社区
这正对应了 Zachary 空手道俱乐部分裂后的两个派别:
社区 A 通常被认为属于 “John A”(俱乐部管理员)派别
社区 B 属于 “Mr. Hi”(空手道教练)派别
研究者 Zachary 在 1970s 的观察中指出,这两个领导者的冲突最终导致俱乐部分裂,成员分别跟随两位领导者。
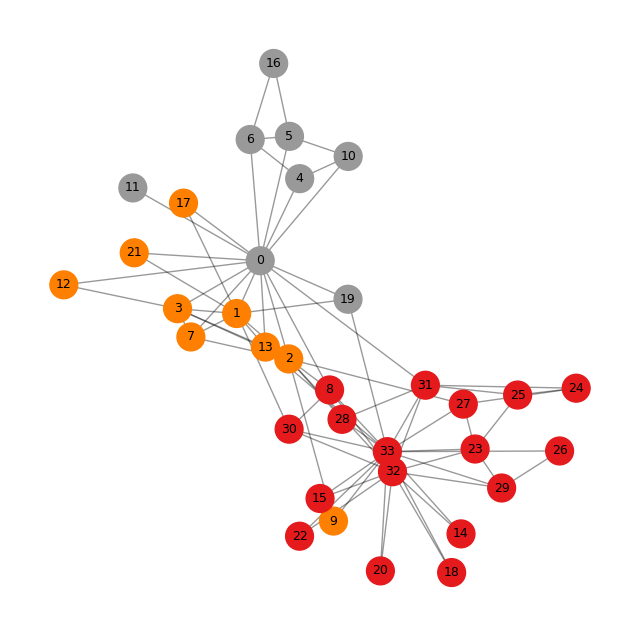
可视化¶
社区上色¶
import networkx as nx
import matplotlib.pyplot as plt
from networkx.algorithms.community import greedy_modularity_communities
# 1. 读入图(空手道俱乐部示例)
G = nx.karate_club_graph()
# 2. 社区检测(这里用 greedy_modularity_communities,适合演示)
communities = list(greedy_modularity_communities(G))
# 3. 给每个节点一个社区编号
node2comm = {}
for i, com in enumerate(communities):
for node in com:
node2comm[node] = i # i 就是社区编号:0,1,2,...
# 4. 准备颜色列表(每个节点对应一个社区编号)
colors = [node2comm[n] for n in G.nodes()]
# 5. 画图:颜色 = 社区编号
plt.figure(figsize=(8, 8))
pos = nx.spring_layout(G, seed=42) # 固定布局,方便反复对比
nx.draw_networkx_nodes(G, pos,
node_color=colors,
cmap=plt.cm.Set1, # 使用一个离散色图
node_size=400)
nx.draw_networkx_edges(G, pos, alpha=0.4)
nx.draw_networkx_labels(G, pos, font_size=9)
plt.axis("off")
plt.show()
热力图¶
import networkx as nx
import matplotlib.pyplot as plt
# 如果你已经有 G 和 bet,可以从这里往下写
# 这里用空手道俱乐部作为示例
G = nx.karate_club_graph()
bet = nx.betweenness_centrality(G)
# 1. 计算布局
pos = nx.spring_layout(G, seed=42) # seed 只是为了每次布局一致
# 2. 把 betweenness 数值取出来
values = list(bet.values())
# 3. 画图
plt.figure(figsize=(6, 6))
# 节点:颜色 = betweenness,大小也随 betweenness 变化
nodes = nx.draw_networkx_nodes(
G,
pos,
node_color=values, # 用 betweenness 当颜色
cmap=plt.cm.OrRd, # 热力图风格颜色(可以改成 viridis, plasma 等)
node_size=[300 + 3000*v for v in values], # 中介中心性越大,节点越大
)
# 边
nx.draw_networkx_edges(G, pos, alpha=0.3)
# 节点标签(显示节点编号)
nx.draw_networkx_labels(G, pos, font_size=8)
# 4. 加一个 colorbar,显示数值含义
cbar = plt.colorbar(nodes)
cbar.set_label("Betweenness centrality")
plt.title("Betweenness centrality heatmap on network")
plt.axis("off")
plt.tight_layout()
plt.show()
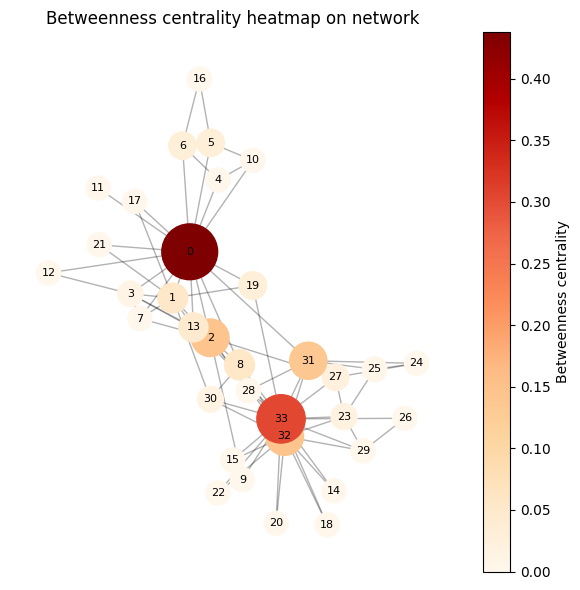
Gephi 美化¶
导出数据
nx.write_gexf(G, "karate_club.gexf")
然后在 Gephi 里进行以下操作:
(1) 打开文件 → Statistics → 运行 “Modularity(模块度)” Gephi 会给节点自动上色,形成两个清晰的社区。
(2) 运行布局算法 → ForceAtlas2 图像会自然展开,呈现两派分离结构。
(3) 设置节点大小 = 度中心性(Degree) 你会看到俱乐部领导者节点会被放大(比如“Mr. Hi”和“Officer”)。