因子分析¶
因子分析是一种多变量统计方法,用于研究多个观测变量之间的相关结构,从中提取出少数几个能够解释这些变量共同变化的潜在因子(latent factors)。
它的基本思想是:
一组高度相关的变量往往受到某些共同潜在因素的影响,因子分析通过数学方法将这些潜在因素提取出来,以揭示数据的内在结构。
因子分析不是为了预测,而是为了“发现结构”。它告诉我们,哪些变量是一类(由同一个潜在因子驱动),以及这些潜在因子各自代表什么。
因子分析步骤¶
1. 数据准备与标准化¶
目的:消除量纲影响,使不同指标可比。
操作:使用 StandardScaler 或 Z-score 标准化。
输出图表:
相关矩阵热图(Correlation Heatmap)
用于直观观察变量间相关性是否较强(适合做因子分析)。
2. 适用性检验¶
目的:判断数据是否适合做因子分析。
操作:
KMO 检验(Kaiser-Meyer-Olkin)
Bartlett 球形检验
结果解释:
KMO > 0.6 表示适合;
Bartlett 检验显著(p < 0.05)表示相关性足够。
输出表格:
KMO 值和 Bartlett 检验结果表。
3. 提取因子(Factor Extraction)¶
目的:确定潜在因子数量。
方法:主成分法(Principal Component)或最大似然法(ML)。
输出图表:
碎石图(Scree Plot):展示特征值(Eigenvalues)的下降趋势,确定拐点位置。
累计方差贡献率图(Cumulative Variance Plot)
4. 因子旋转(Factor Rotation)¶
目的:让因子结构更清晰(每个变量主要载荷在一个因子上)。
方法:常用 Varimax(正交旋转)或 Oblimin(斜交旋转)。
输出表格:
因子载荷矩阵(Factor Loadings Table)
若有旋转前后对比,也可输出两张表比较。
输出图表:
因子载荷热图(Factor Loadings Heatmap)
用颜色显示变量在不同因子上的载荷强度。
5. 因子得分计算(Factor Scores)¶
目的:计算每个样本在各因子上的得分。
输出图表:
因子得分散点图(Factor Score Scatter Plot)
可用前两个因子作坐标轴,展示样本聚类特征。
6. 因子解释与命名¶
目的:根据高载荷变量解释每个因子的含义。
输出表格:
因子命名表(列出每个因子对应的高载荷变量及解释)。
可视化图表总结表¶
步骤 |
图表类型 |
图表内容 |
工具(Python) |
|---|---|---|---|
1 |
相关矩阵热图 |
各变量之间的相关性 |
sns.heatmap(corr) |
2 |
KMO & Bartlett表 |
检验统计结果 |
factor_analyzer.calculate_kmo, calculate_bartlett_sphericity |
3 |
碎石图 |
特征值趋势确定因子数 |
plt.plot(eigenvalues) |
3 |
累计方差贡献图 |
解释方差占比 |
plt.bar() |
4 |
因子载荷热图 |
各变量在因子上的权重 |
sns.heatmap(loadings) |
5 |
因子得分散点图 |
样本分布 |
plt.scatter(scores[:,0], scores[:,1]) |
6 |
因子解释表 |
各因子的含义说明 |
pd.DataFrame |
代码¶
# =========================================================
# 因子分析(以 winequality-red.csv 为例,Seaborn 绘图版)
# 特点:
# - 中文注释 + 英文图表
# - 包含 Correlation Heatmap
# - Scree Plot 含累计方差曲线与红线(Eigenvalue=1)
# - 因子提取与 Varimax 旋转
# =========================================================
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import FactorAnalysis
# -----------------------------
# 0) 数据读取与预处理
# -----------------------------
sns.set_theme(style="whitegrid")
CSV_PATH = "winequality-red.csv" # 请修改为你的路径
if not os.path.exists(CSV_PATH):
raise FileNotFoundError("请将 winequality-red.csv 放在脚本同目录下。")
# 读取 UCI 红酒数据(分号分隔),仅保留数值列
df = pd.read_csv(CSV_PATH, sep=";").select_dtypes(include=[np.number]).dropna()
cols = df.columns.tolist()
p = len(cols)
# 标准化数据
scaler = StandardScaler()
X_std = scaler.fit_transform(df)
R = np.corrcoef(X_std, rowvar=False)
n = X_std.shape[0]
# -----------------------------
# 1) 相关性热图 (Correlation Matrix Heatmap)
# -----------------------------
# 说明:因子分析前通常需查看变量之间的相关程度
plt.figure(figsize=(0.45 * p + 3, 0.45 * p + 3))
ax = sns.heatmap(pd.DataFrame(R, index=cols, columns=cols),
cmap="coolwarm", vmin=-1, vmax=1, square=True,
annot=True, fmt=".2f", cbar=True)
ax.set_title("Correlation Matrix Heatmap", fontsize=14)
ax.set_xticklabels(ax.get_xticklabels(), rotation=45, ha="right")
ax.set_yticklabels(ax.get_yticklabels(), rotation=0)
plt.tight_layout()
plt.show()
# -----------------------------
# 2) 特征值分析 (Scree Plot + Cumulative Variance)
# -----------------------------
# 说明:分析相关矩阵的特征值以确定因子数量
evals, evecs = np.linalg.eigh(R)
evals = np.sort(evals)[::-1]
cumvar = np.cumsum(evals) / np.sum(evals)
plt.figure(figsize=(7, 5))
# 绘制特征值曲线
ax1 = sns.lineplot(x=range(1, p + 1), y=evals, marker="o",
label="Eigenvalue", color="steelblue")
# 红线:Eigenvalue = 1
plt.axhline(1.0, color="red", linestyle="--", linewidth=1.2, label="Eigenvalue = 1")
# 累积方差曲线(右轴)
ax2 = plt.twinx()
sns.lineplot(x=range(1, p + 1), y=cumvar, marker="s",
label="Cumulative Variance", color="orange", ax=ax2)
ax2.set_ylabel("Cumulative Variance", fontsize=11)
ax2.set_ylim(0, 1.05)
# 标题与轴标签
ax1.set_title("Scree Plot with Cumulative Variance", fontsize=14)
ax1.set_xlabel("Component number", fontsize=11)
ax1.set_ylabel("Eigenvalue", fontsize=11)
ax1.grid(True, linestyle="--", alpha=0.5)
# 合并图例
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()
ax1.legend(h1 + h2, l1 + l2, loc="best")
plt.tight_layout()
plt.show()
# -----------------------------
# 3) 因子提取 (Factor Extraction)
# -----------------------------
# 说明:使用 Kaiser 规则 (eigenvalue > 1) 选择因子数
n_factors = int(np.sum(evals > 1.0))
n_factors = max(2, min(n_factors, 6))
print(f"Selected number of factors: {n_factors}")
# 使用最大似然法提取因子
fa = FactorAnalysis(n_components=n_factors, random_state=42)
fa.fit(X_std)
loadings = fa.components_.T # (p, k)
# -----------------------------
# 4) Varimax 旋转 (Rotation)
# -----------------------------
def varimax(Phi, gamma=1.0, q=20, tol=1e-6):
"""Kaiser (1958) Varimax 旋转:使载荷更稀疏,便于解释"""
p, k = Phi.shape
R = np.eye(k)
d = 0.0
for _ in range(q):
d_old = d
Lambda = Phi @ R
u, s, vh = np.linalg.svd(
Phi.T @ (Lambda**3 - (gamma/p) * (Lambda @ np.diag(np.sum(Lambda**2, axis=0))))
)
R = u @ vh
d = np.sum(s)
if d_old != 0 and d / d_old < 1.0 + tol:
break
return Phi @ R
rot_loadings = varimax(loadings)
loadings_df = pd.DataFrame(rot_loadings,
index=cols,
columns=[f"Factor_{i+1}" for i in range(n_factors)]).round(3)
print("\nRotated Factor Loadings (head):")
print(loadings_df.head())
# 可视化:旋转换荷热图(英文标签)
plt.figure(figsize=(1.8 * n_factors + 3, 0.45 * p + 3))
sns.heatmap(loadings_df, cmap="coolwarm", center=0, annot=True, fmt=".2f")
plt.title("Factor Loadings Heatmap (Varimax rotated)", fontsize=14)
plt.tight_layout()
plt.show()
# -----------------------------
# 5) 因子得分散点图(F1 vs F2)
# -----------------------------
# 若有分组列(如 quality),用于上色;否则不分组
plot_df = scores_df.copy()
if group_col is not None:
plot_df[group_col] = df_num[group_col].values
plt.figure(figsize=(7, 5))
if group_col is not None:
# 按质量分组上色(离散色板)
sns.scatterplot(
data=plot_df, x="F1", y="F2",
hue=group_col, palette="viridis", s=25, alpha=0.7, edgecolor=None
)
plt.legend(title=group_col, bbox_to_anchor=(1.02, 1), loc="upper left")
else:
# 不分组的简单散点
sns.scatterplot(
data=plot_df, x="F1", y="F2",
s=25, alpha=0.7, edgecolor=None
)
# 英文坐标轴与标题
plt.axhline(0, linestyle="--", linewidth=0.8, alpha=0.6)
plt.axvline(0, linestyle="--", linewidth=0.8, alpha=0.6)
plt.title("Factor Scores Scatter (F1 vs F2)", fontsize=14)
plt.xlabel("Factor 1 score")
plt.ylabel("Factor 2 score")
plt.tight_layout()
plt.show()
图表分析¶
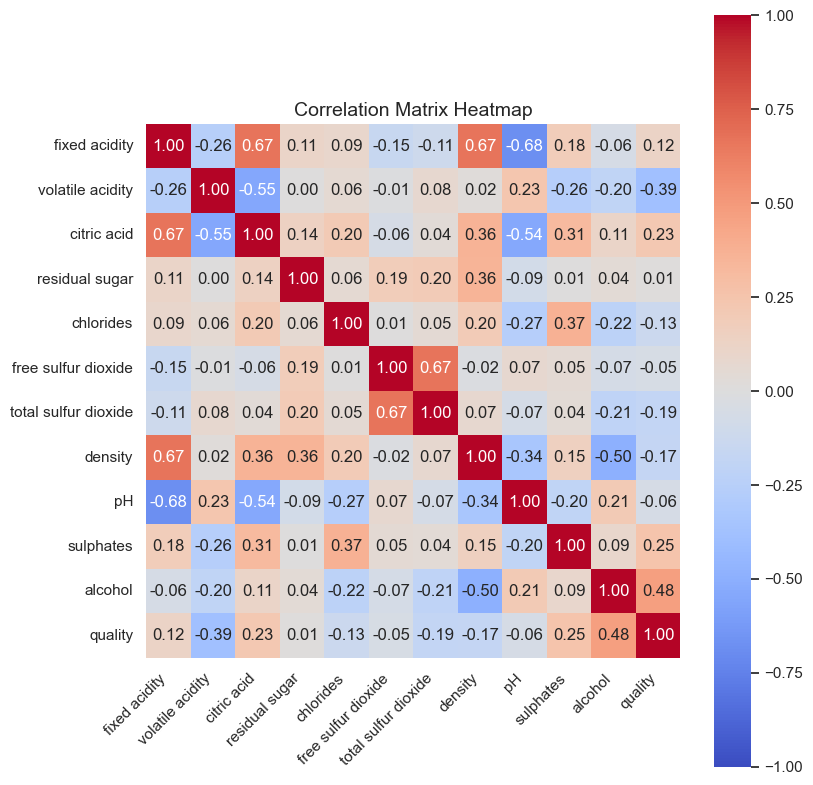
相关性热力图¶
大多数变量间相关系数 > 0.3,则说明有共同特征 ,这说明可做因子分析。
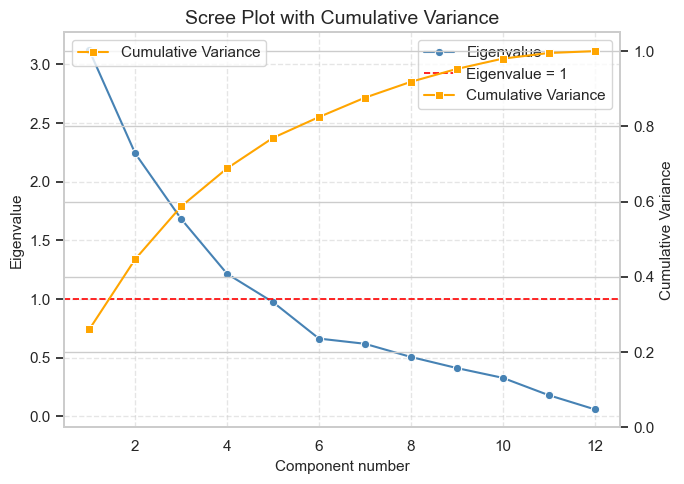
碎石图(Scree Plot)¶
用于帮助判断因子分析或主成分分析中应当提取多少个因子(或主成分)
Selected number of factors: 4
Rotated Factor Loadings (head):
Factor_1 Factor_2 Factor_3 Factor_4
fixed acidity 0.990 0.004 -0.097 -0.083
volatile acidity -0.194 -0.168 0.048 0.700
citric acid 0.639 0.130 0.066 -0.553
residual sugar 0.145 0.076 0.226 0.044
chlorides 0.085 -0.231 0.030 -0.187
从图中可以看到三条关键信息:
蓝线(Eigenvalue):显示每个成分解释的方差量。
橙线(Cumulative Variance):显示累计解释的方差比例。
红线(Eigenvalue = 1):表示 Kaiser 规则的阈值。
如果你沿着橙线往上看,会发现:
到 第 3 个成分,累计方差大约在 60% 左右;
到 第 4 个成分,累计方差上升到 约 70%;
此后增长幅度变缓。
如何判断应该取多少个因子
方法 |
含义 |
实际应用建议 |
|---|---|---|
Kaiser 规则 |
保留特征值 > 1 的因子 |
从图上看,前 4 个因子均 > 1,因此建议取 4 因子。 |
碎石图拐点法 (Elbow) |
找到蓝线弯折明显处 |
蓝线在第 4 个点之后趋于平缓,也支持 4 因子。 |
累计方差解释率 |
累计方差应达到 60–70% |
到第 4 个因子约 70%,解释力较好。 |
综合三者判断:
这张图显示 取 4 个因子是合理选择。 前 4 个因子能共同解释约 70% 的方差,之后的成分增益已经非常小。
因子载荷矩阵¶
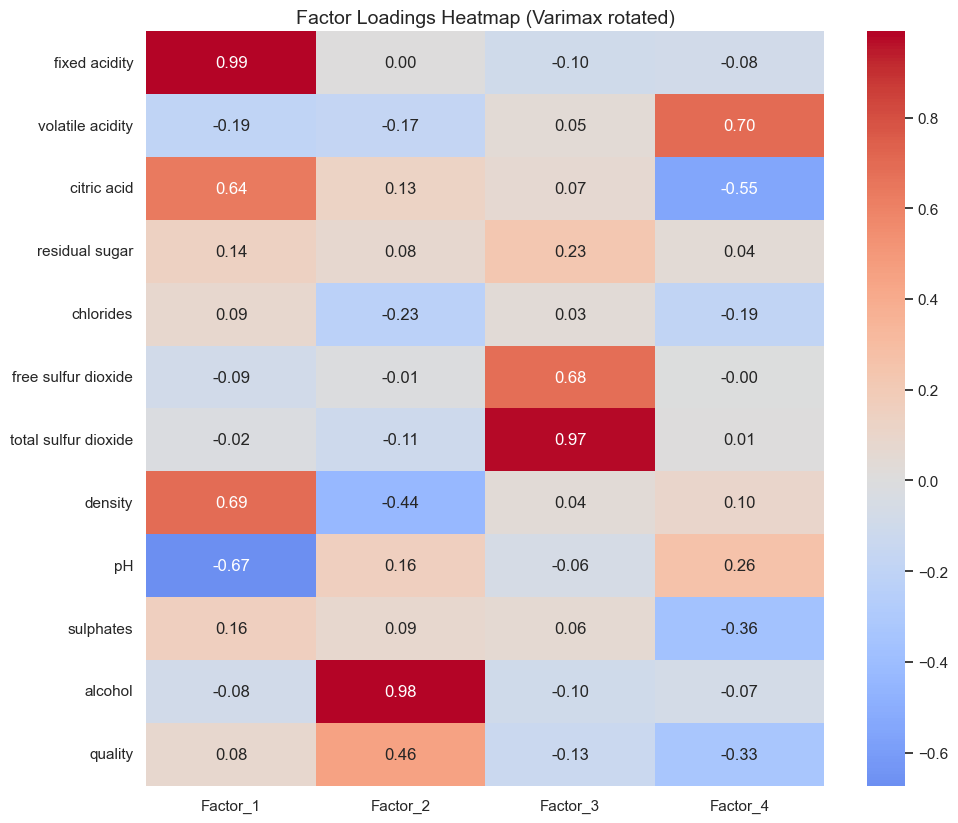
图的含义¶
纵轴(行):每一个观测变量(红酒的化学特征,如酸度、酒精度、硫含量等)
横轴(列):提取出的 4 个因子(Factor_1 ~ Factor_4)
颜色:表示载荷(loading)的大小和方向
红色(接近 +1):该变量与该因子强烈正相关
蓝色(接近 -1):强烈负相关
接近 0:几乎无关联
数值:每个单元格的载荷值(一般 |loading| > 0.5 视为显著相关)
找“高载荷”的变量群¶
每个因子(列)通常会有若干变量载荷显著高(红色或蓝色明显)。
这些变量共同反映了该因子的潜在含义。
因子 |
高载荷变量 |
含义解释(推测) |
|---|---|---|
Factor_1 |
fixed acidity (+0.99), citric acid (+0.64), density (+0.69), pH (-0.67) |
酸度因子 (Acidity Factor):酸度越高,密度越大,pH 越低(酸性更强) |
Factor_2 |
alcohol (+0.98), quality (+0.46), density (-0.44) |
酒精与品质因子 (Alcohol & Quality Factor):酒精度高的酒通常品质评分更高、密度更低 |
Factor_3 |
total sulfur dioxide (+0.97), free sulfur dioxide (+0.68) |
硫化物防腐因子 (Sulfur Preservation Factor):表示与亚硫酸盐防腐相关的变量群 |
Factor_4 |
volatile acidity (+0.70), citric acid (-0.55), sulphates (-0.36) |
挥发与芳香因子 (Volatile/Aromatic Factor):与酸香气、易挥发物质相关 |
从热图观察结构¶
Factor_1(最左列)呈现强烈红色的固定酸度和密度,同时蓝色的 pH,说明这些变量构成一个统一维度(酸度结构)。
Factor_2 以酒精度(alcohol)为主导,是最单一、最强的因子。
Factor_3 明显由两类硫酸盐变量组成,代表保存性。
Factor_4 较为复杂,有正有负,可能与香气和风味特征相关。
阅读技巧¶
看颜色块的聚集:相邻红块说明这些变量属于同一个因子维度;
看蓝红相反方向:说明变量在该维度上呈相反关系(如 pH 与 acidity)。
忽略接近 0 的浅灰格:它们在该因子上贡献不显著。
简要总结¶
因子 |
代表意义 |
主要高载荷变量 |
|---|---|---|
Factor 1 |
Acidity & Density |
fixed acidity (+), citric acid (+), pH (-) |
Factor 2 |
Alcohol & Quality |
alcohol (+), quality (+), density (-) |
Factor 3 |
Sulfur Compounds |
total sulfur dioxide (+), free sulfur dioxide (+) |
Factor 4 |
Volatile Aromas |
volatile acidity (+), citric acid (-), sulphates (-) |
因子得分散点图(Factor Scores Scatter Plot)¶
因子得分散点图(Factor Scores Scatter Plot),展示了每个样本(每瓶红酒)在前两个因子上的位置与分布。我们可以从三个层面来解读这张图。
图的结构含义¶
• 横轴 (Factor 1 score):样本在第 1 个因子上的得分。
得分高 → 在该因子上具有更强的特征;得分低 → 特征较弱或相反。 • 纵轴 (Factor 2 score):样本在第 2 个因子上的得分。 • 颜色 (quality):红酒品质等级。颜色越亮代表质量分数越高。
每个点代表一瓶酒,它的坐标是 (F1_score, F2_score),颜色反映酒的质量等级。
如何解读得分分布¶
点的集中区域 大部分样本分布在中心(0, 0)附近,说明大部分酒在这两个潜在维度上比较“平均”,没有极端特征。
四象限解读 • 右上象限(F1、F2 都高):在两个因子上得分都高的酒,可能同时具备高酸度与高酒精度(取决于因子定义)。 • 右下象限(F1 高、F2 低):在 Factor 1 维度上突出,但在 Factor 2 上较弱。 • 左上象限(F1 低、F2 高):与上相反,第二个因子特征强。 • 左下象限(两者都低):在两个维度上特征都弱的酒。
颜色梯度的意义 • 颜色由深到浅(3 → 8)代表品质从低到高。 • 如果亮色点(高 quality)倾向集中在某个区域,比如右上象限,说明那一类因子组合对应的酒更高质量。 • 例如:若右上方主要是亮黄点,而左下方是深蓝点,则说明“高 F1 + 高 F2”型酒质量更好。
结合前面的因子解释¶
假设:
Factor 1 是“酸度因子 (Acidity)”
Factor 2 是“酒精与品质因子 (Alcohol & Quality)”
那么图的含义可解释为:
横轴越右 → 酸度越高; 纵轴越上 → 酒精度和综合品质越高。
若高质量酒集中在右上方,就意味着:
“酸度适中 + 酒精度较高” 的酒在感官评分中更受欢迎。
因子解释与命名¶
# =========================================================
# 6) 因子解释与命名(中文版输出)
# =========================================================
# 设置高载荷阈值
threshold = 0.5
# 提取每个因子对应的高载荷变量
factor_dict = {}
for factor in loadings_df.columns:
high_vars = loadings_df.index[loadings_df[factor].abs() >= threshold].tolist()
factor_dict[factor] = high_vars
# 生成因子命名表(自动提取前三个代表变量,可人工修改命名)
factor_names = []
factor_meanings = []
for i, (factor, vars_) in enumerate(factor_dict.items(), start=1):
name_guess = "、".join(vars_[:3]) if vars_ else "无显著载荷变量"
factor_names.append(f"因子 {i}")
factor_meanings.append(f"主要变量:{name_guess}")
factor_table = pd.DataFrame({
"因子编号": factor_names,
"高载荷变量": factor_dict.values(),
"解释说明(可人工修改)": factor_meanings
})
print("\n【因子命名表】")
display(factor_table)
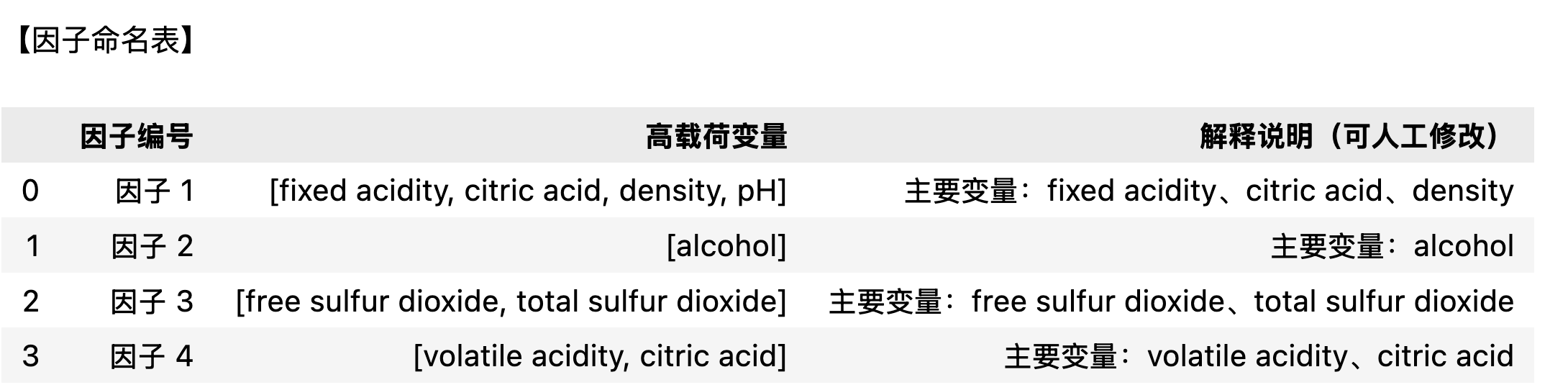
命名的基本逻辑¶
人类专家命名时,通常遵循以下三步:
找出每个因子的高载荷变量
即载荷绝对值较高(一般 ≥0.5)的变量。
这些变量反映了因子在数据中“代表的主题”。
识别这些变量的共性
它们是否都描述某个化学性质、感官特征或保存方式?
例如:如果包含 fixed acidity, citric acid, pH,很可能和“酸度”有关。
给出一个简洁、有意义的标签(命名)
名称要能总结该组变量的核心含义。
名称可视报告语言而定。
逐个因子的命名思路¶
因子编号 |
高载荷变量 |
专家判断逻辑 |
建议命名 |
|---|---|---|---|
因子 1 |
fixed acidity, citric acid, density, pH |
这些变量都与酸度和密度有关,且 pH 与酸度呈负相关。说明该因子反映了酸度结构。 |
酸度因子 (Acidity Factor) |
因子 2 |
alcohol |
只有酒精度高载荷,说明该因子几乎完全反映酒精含量的差异。 |
酒精因子 (Alcohol Factor) |
因子 3 |
free sulfur dioxide, total sulfur dioxide |
这两个指标都与防腐和保存有关(SO₂ 是防腐剂)。 |
防腐因子 / 硫化物因子 (Sulfur Preservation Factor) |
因子 4 |
volatile acidity, citric acid |
挥发性酸与芳香酸度有关,反映了红酒的香气与风味特征。 |
芳香因子 / 挥发性酸因子 (Aroma / Volatile Factor) |
命名时应避免的常见错误¶
错误做法 |
问题 |
改进建议 |
|---|---|---|
直接用变量名当因子名 |
太机械,缺乏解释性 |
提炼共同概念,如“酸度因子” |
过度主观化 |
未基于变量含义,而凭感觉命名 |
必须有变量层面的证据支撑 |
命名太长 |
难以记忆与报告引用 |
控制在 2–4 个词以内 |
正式报告写法(中英双语范例)¶
因子解释与命名(Factor Interpretation and Naming)
根据旋转后的因子载荷结果,研究者依据高载荷变量的化学意义,对四个因子进行了如下解释与命名:
酸度因子(Acidity Factor):主要由 fixed acidity、citric acid、density 和 pH 构成,代表红酒的酸度结构特征。
酒精因子(Alcohol Factor):由 alcohol 主导,反映酒精含量差异。
防腐因子(Sulfur Preservation Factor):由 free sulfur dioxide 和 total sulfur dioxide 构成,描述红酒防腐与稳定性。
芳香因子(Aroma / Volatile Factor):由 volatile acidity 与 citric acid 组成,反映挥发性酸与芳香物质特征。