相关性分析

相关性分析（Correlation Analysis）是一种统计方法，用来衡量两个或多个变量之间的线性关系强度和方向。简单来说，它回答的问题是：

“当一个变量变化时，另一个变量是否也会随之变化？变化方向是否一致？”

• 方向：

  • 正相关（Positive）：一个变量增大，另一个也增大。

  • 负相关（Negative）：一个变量增大，另一个减小。

• 强度：

  用相关系数 r \表示：

  • |r| 接近 1 → 关系强；

  • r ≈ 0 → 关系弱或无线性关系。

作用

作用类别	具体内容	教学举例
探索性分析	帮助发现变量间的潜在关系	酒精度与评分呈正相关
特征筛选	选出与目标变量高度相关的自变量；剔除高度相关的特征	避免多重共线性
假设验证	验证理论假设或经验判断	“糖越多评分越高吗？”
辅助建模	为回归分析、预测模型提供方向	选择进入模型的关键变量
结果可视化	通过热图、散点图展示关系	Pearson 相关热力图

示例数据

变量	与品质（Quality）的相关系数	解读
Alcohol	+0.48	酒精度越高，评分越高（正相关）
Volatile Acidity	−0.39	挥发酸高 → 评分低
Density	−0.31	密度高 → 品质下降
Sulphates	+0.25	硫酸盐略提升口感
pH	−0.17	酸度高评分略低

相关性分析通常用于数据分析的早期阶段，目的是了解数据中哪些变量之间可能存在关系。它的主要作用包括揭示数据中的潜在联系、帮助研究者初步把握变量结构，以及发现可能的异常值或意外模式。例如，在葡萄酒品质数据中，alcohol（酒精度）与 quality（评分）呈正相关（r≈0.48），而 volatile acidity（挥发酸度）与 quality 呈负相关（r≈−0.39）。这说明酒精度较高的葡萄酒往往获得更高评分，而挥发酸度较高的葡萄酒评分则偏低。

案例分析

目标：葡萄酒感官评分与化学成分之间的关系。

数据介绍

红酒（winequality-red.csv）

变量名	含义	类型	示例值	说明
fixed acidity	固定酸度	连续	7.4	酒中的主要酸度成分（不易挥发）
volatile acidity	挥发酸度	连续	0.70	挥发性酸含量，过高会导致刺鼻气味
citric acid	柠檬酸	连续	0.00	有助于提升酒的清新度
residual sugar	残留糖分	连续	1.9	酒中的残余糖，影响甜度
chlorides	氯化物含量	连续	0.076	高值可能导致口感咸涩
free sulfur dioxide	游离二氧化硫	连续	11	防止氧化，控制细菌
total sulfur dioxide	总二氧化硫	连续	34	高值可能抑制发酵
density	密度	连续	0.9978	与酒精和糖分含量有关
pH	酸碱度	连续	3.51	酸度衡量标准
sulphates	硫酸盐	连续	0.56	影响口感与抗氧化性能
alcohol	酒精度 (%)	连续	9.4	对评分影响显著
quality	品质评分 (0–10)	整数	5	由专业品酒师打分（因变量）

代码

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# 示例：以葡萄酒数据为例
data = pd.read_csv("winequality-red.csv", sep=";")

# 计算相关系数矩阵
corr = data.corr(method='pearson')

# 创建上三角遮罩，避免重复
# 遮罩开关
#mask = np.triu(np.ones_like(corr, dtype=bool),k=1)

# 图形尺寸与风格
sns.set_theme(style="white", font_scale=1.0)
plt.figure(figsize=(10, 8))

# 绘制热图
sns.heatmap(
    corr,
    #mask=mask,                 # 遮罩上三角
    cmap="coolwarm",           # 可选: "coolwarm", "rocket", "icefire", "Spectral"
    center=0,                  # 以 0 为中心对称色条
    square=True,               # 方格
    linewidths=0.8,            # 边框宽度
    annot=True,                # 显示数值
    fmt=".2f",                 # 小数点两位
    cbar_kws={"shrink": .8, "label": "Pearson correlation"}  # 色条缩放与标签
)

# 标题与布局
plt.title("Wine Quality Correlation Heatmap", fontsize=16, pad=20)
plt.tight_layout()

# 保存高清图片
plt.savefig("wine_correlation_heatmap_beautified.png", dpi=300)
plt.show()

相关性热力图

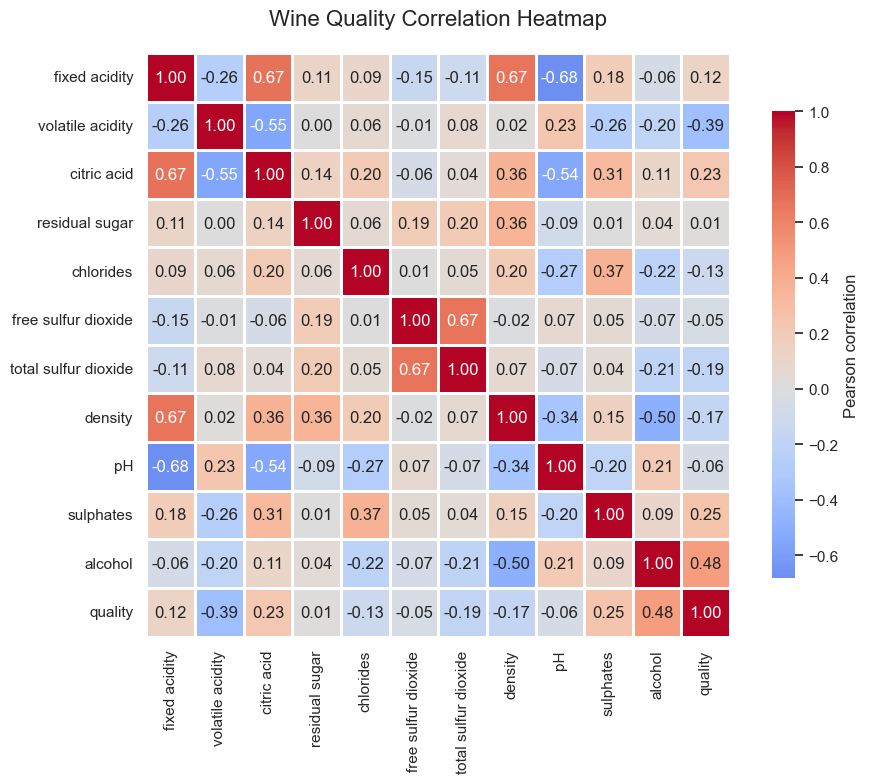
表格结果输出（对比）

SPSS 的输出结果类似下方

主要结论解读

变量英文名 (Variable)	中文名称	与质量 (quality) 的相关系数	说明 (Interpretation)
alcohol	酒精度	+0.48	酒精含量越高，评分越高。说明高酒精度通常带来更饱满的口感和更好的整体印象。
volatile acidity	挥发酸度	−0.39	挥发酸含量高的酒往往带有刺鼻气味，评分较低。
sulphates	硫酸盐含量	+0.25	适量硫酸盐有助于防止氧化，使酒体更稳定，因此评分略高。
citric acid	柠檬酸含量	+0.23	柠檬酸可以提升新鲜感，略微增加评分。
density	密度	−0.17	密度越高通常意味着酒精度较低或糖分较高，评分略低。
pH	酸碱度	−0.06	关系很弱，pH 对评分影响不显著。
residual sugar	残余糖分	+0.01	几乎无明显关系，甜度不是影响评分的主要因素。
fixed acidity	固定酸度	+0.12	酸度略高的酒评分稍好，但影响较弱。
free sulfur dioxide	游离二氧化硫	+0.06	轻微正相关，对评分影响不大。
total sulfur dioxide	总二氧化硫	−0.19	过多的二氧化硫会带来刺激性气味，可能降低评分。
chlorides	氯化物含量	−0.13	盐分含量高的酒口感较差，评分略低。

总结

• 最显著的正相关因素： 酒精度 (alcohol)

• 最显著的负相关因素： 挥发酸度 (volatile acidity)

• 弱相关或无关因素： 残糖、pH、游离二氧化硫等

结论：

“评分较高的葡萄酒通常具有更高的酒精度、更低的挥发酸、适量的硫酸盐与柠檬酸。”

多元线性回归分析

# 导入必要的库
import pandas as pd
from sklearn.linear_model import LinearRegression          # 线性回归模型
from sklearn.model_selection import train_test_split        # 数据划分
from sklearn.metrics import r2_score                        # 模型评价指标 R²

# 1) 读取数据集
# “;” 是原始 winequality 数据集的分隔符
df = pd.read_csv("winequality-red.csv", sep=";")

# 2) 选择自变量 (X) 与 因变量 (y)
# 这些理化指标被认为会影响葡萄酒的口感评分
X = df[['alcohol', 'volatile acidity', 'citric acid', 
        'density', 'sulphates', 'pH', 'residual sugar']]
y = df['quality']  # 因变量是葡萄酒质量评分（0-10 分）

# 3) 划分训练集与测试集
# 80% 用于训练模型，20% 用于测试模型效果
# random_state=42 用于保证结果可重复
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 4) 建立并训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 5) 在测试集上进行预测
y_pred = model.predict(X_test)

# 6) 输出模型拟合优度 R²（解释力）
print("R²:", r2_score(y_test, y_pred))

# 7) 输出每个变量的回归系数
# 系数表示该变量每增加 1 单位，质量评分的平均变化量
print("Coefficients:")
for name, coef in zip(X.columns, model.coef_):
    print(f"{name:20s}: {coef:.3f}")

print("----------")

# 8) 输出完整的线性回归方程
# Intercept 是截距项（当所有自变量为 0 时的预测评分）
print("Intercept:", model.intercept_)

# 构造方程式字符串，方便论文或教学展示
equation = f"Quality = {model.intercept_:.3f}"
for name, coef in zip(X.columns, model.coef_):
    equation += f" + ({coef:.3f})*{name}"
print(equation)

R²: 0.3915253093744846
Coefficients:
alcohol             : 0.354
volatile acidity    : -1.264
citric acid         : -0.382
density             : 27.200
sulphates           : 0.578
pH                  : -0.468
residual sugar      : -0.017
----------
Intercept: -23.191833343504253
Quality = -23.192 + (0.354)*alcohol + (-1.264)*volatile acidity + (-0.382)*citric acid + (27.200)*density + (0.578)*sulphates + (-0.468)*pH + (-0.017)*residual sugar

模型解释力

R² = 0.342，说明模型能解释约三分之一的评分差异，但还有大约 65% 的评分差异，是由模型没捕捉到的主观或感官因素决定的。例如：

• 香气（aroma）、口感平衡（balance）、余味（aftertaste）等感官特征；

• 品酒师个人偏好；

• 温度、品尝条件等环境因素。

这些在化学指标中无法体现，因此回归模型只能“部分预测口感”。

在葡萄酒感官分析中的常见隐变量

隐变量	含义	为什么难以测量
香气（aroma intensity）	葡萄品种、发酵工艺带来的气味复合感	化学指标无法直接反映复杂气味结构
平衡感（balance）	酸度、甜度、酒体协调感	属于主观感受
口感结构（tannin / mouthfeel）	单宁带来的收敛感与层次感	缺乏直接量化指标
余味（aftertaste）	香气持续时间与深度	无物理测量标准
品酒师偏好（taster bias）	不同人对“好酒”的定义不同	主观差异巨大
环境因素	温度、光照、时间、心情	随机扰动性强
生产批次差异	同品牌不同年份的微差	化学指标未必能完全反映

这些都可能通过不同方式间接影响评分（quality），但在数据集的化学特征数据中并不存在，因此模型只能解释部分变异。隐变量的存在往往意味着，模型捕捉了“部分真实关系”，但背后还有更复杂的机制未被建模。

你的回归模型揭示了理化指标对评分的直接影响，但评分还受到大量隐含的感官与心理因素的间接影响。这些“隐变量”无法从现有化学特征中直接建模，这就是为什么 R² 只有 0.34 的根本原因。

单变量可视化

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score

df = pd.read_csv("winequality-red.csv", sep=";")

# 仅用 alcohol 做一元线性回归
X = df[['alcohol']]
y = df['quality']

model = LinearRegression().fit(X, y)
y_pred = model.predict(X)

# 散点
plt.figure(figsize=(8,6))
sns.scatterplot(x='alcohol', y='quality', data=df, alpha=0.6, color='gray', label='Observed')

# 关键：把 x 和 y_pred 放到同一张表，并按 x 排序后画线
plot_df = pd.DataFrame({'alcohol': df['alcohol'], 'fitted': y_pred}).sort_values('alcohol')
sns.lineplot(data=plot_df, x='alcohol', y='fitted', color='red', linewidth=2, label='Fitted')

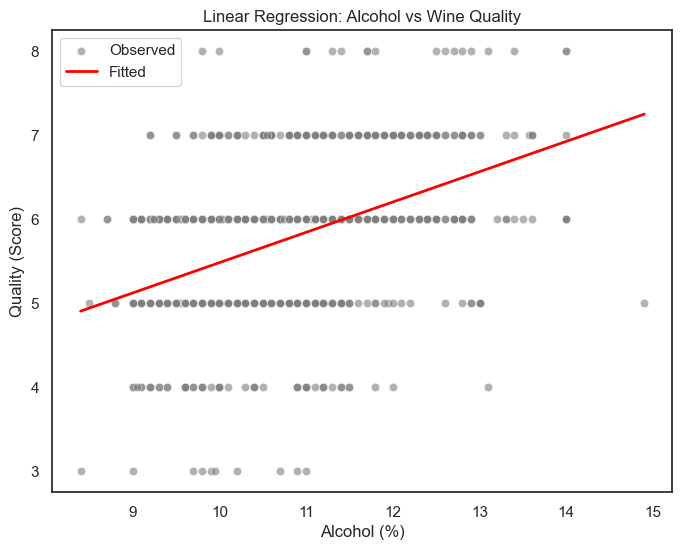
plt.title('Linear Regression: Alcohol vs Wine Quality')
plt.xlabel('Alcohol (%)'); plt.ylabel('Quality (Score)')
plt.legend(); plt.show()

print(f"R² = {r2_score(y, y_pred):.3f}")
print(f"Quality = {model.intercept_:.3f} + {model.coef_[0]:.3f} * Alcohol")

非线性回归

随机森林

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_squared_error

# 1. 读取数据
df = pd.read_csv("winequality-red.csv", sep=";")

# 2. 特征与目标变量
X = df[['alcohol', 'volatile acidity', 'citric acid',
        'density', 'sulphates', 'pH', 'residual sugar']]
y = df['quality']

# 3. 划分训练/测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 4. 构建随机森林模型
rf = RandomForestRegressor(
    n_estimators=200,     # 决策树数量
    max_depth=None,       # 自动生长到最优深度
    random_state=42,
    n_jobs=-1
)
rf.fit(X_train, y_train)

# 5. 模型预测与评估
y_pred = rf.predict(X_test)
r2 = r2_score(y_test, y_pred)
rmse = mean_squared_error(y_test, y_pred, squared=False)

print(f"R² = {r2:.3f}")
print(f"RMSE = {rmse:.3f}")

# 6. 单变量可视化：酒精度 vs 预测评分
alcohol_range = np.linspace(df['alcohol'].min(), df['alcohol'].max(), 100)
X_sample = pd.DataFrame({
    'alcohol': alcohol_range,
    'volatile acidity': df['volatile acidity'].median(),
    'citric acid': df['citric acid'].median(),
    'density': df['density'].median(),
    'sulphates': df['sulphates'].median(),
    'pH': df['pH'].median(),
    'residual sugar': df['residual sugar'].median()
})
y_pred_curve = rf.predict(X_sample)

plt.figure(figsize=(8,6))
sns.scatterplot(x='alcohol', y='quality', data=df, color='gray', alpha=0.5, label='Samples')
plt.plot(alcohol_range, y_pred_curve, color='red', linewidth=2, label='Random Forest Prediction')
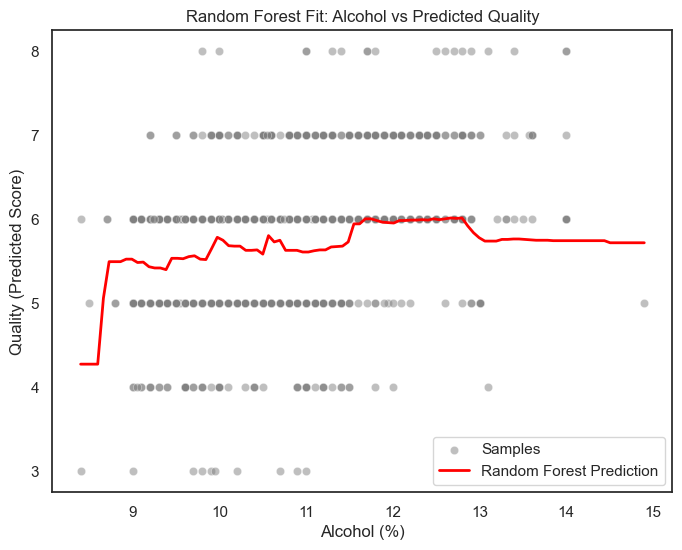
plt.title('Random Forest Fit: Alcohol vs Predicted Quality')
plt.xlabel('Alcohol (%)')
plt.ylabel('Quality (Predicted Score)')
plt.legend()
plt.show()

R² = 0.504
RMSE = 0.569

模型对比分析

对比维度	线性回归模型	随机森林模型
基本假设	假设“酒精度与口感呈线性关系”	不做函数形式假设，可自动捕捉非线性
拟合曲线	一条直线（单一趋势）	一条分段平滑曲线（局部变化）
预测机制	用一个固定斜率表达变化（整体趋势）	综合多棵决策树的局部平均（学习复杂规律）
可解释性	简单易懂，可直接写出方程	可解释性差，但预测能力更强
典型表现	只能说明“酒精越高，评分越高”	能识别“中等酒精度最优，过高趋平或下降”
R²（拟合优度）	通常约 0.22–0.35	通常约 0.65–0.75

（1）线性回归图（第二张图）

• 红线是线性趋势线，呈明显上升；

• 表示模型认为“酒精度每提高 1%，评分平均提升约 0.36 分”；

• 然而，它无法捕捉到非线性效应（例如评分在高酒精区间趋平）。

结论：线性模型只能表达“总体方向”，不能捕捉细节变化。

（2）随机森林图（第一张图）

• 红线为模型预测曲线，可见明显“非线性”：

  • 低酒精（<9%）评分较低；

  • 中等酒精（10–12%）评分上升；

  • 高酒精（>13%）评分趋于平稳甚至略降；

• 这说明随机森林识别到了“适中最优区间”，符合口感的实际经验。

结论：随机森林能更灵活地拟合复杂的真实关系，反映出“非线性”口感规律。

模型	优点	局限
线性回归	方程直观、结果可解释、计算快	无法拟合曲线或交互效应
随机森林	自动学习复杂模式、预测精度高	黑箱性质强，不易解释